L’hypothèse du mathématicien Benoît Mandelbrot résidait dans la capacité des marchés à avoir des comportements distincts mais reliés selon les époques. En conséquence, cela revient à écrire que les marchés financiers sont déterminés par des cycles précis et que le temps a une grande influence sur les schémas de prix. Dans ses ouvrages, Benoît Mandelbrot parlait également « d’auto force relative » pour parler des fractales et de la mesure de leur importance. Dans notre précédente publication, nous avons dédié nos écrits à l’interprétation du coefficient de Hurst (Exposant de Hurst en finance – Youtrading FR). Désormais, on s’attachera à simplifier autant que possible la mesure des fractales, qui en vérité, se résument à deux lignes de calcul. Deux lignes dont l’impact sur le monde financier est total et omniprésent. 

Hypothèse de non-stationnarité (ou de cyclicité) des marchés…

Jusqu’ici, les analystes avaient l’habitude de décrire les marchés par des volatilités et des probabilités qui s’appliquaient théoriquement sur des échelles de temps plus longues, sans aucune influence de la période et du temps. De sorte, cela revenait à dire que les évolutions futures du cours d’un actif étaient congénitalement indépendantes des variations passées (discontinuité). Pour Benoît Mandelbrot au contraire, les évolutions futures des marchés étaient décrites dans une petite fraction des cours du passé, de sorte que l’évolution future des prix était déterminée par des cycles précis. Cela implique que les probabilités d’une période à l’autre sont « biaisées » (« non-stationnaires ») et qu’il existe bien des dynamiques relativement déterministes. En ce sens, les fractales sont directement liées aux cycles de marché.

Dans son ouvrage de référence, le mathématicien Benoît Mandelbrot, à l’origine de la compréhension des fractales, rappelle la conséquence de la découverte de la non-stationnarité en finance : 

« Les variations au jour le jour du prix du marché avaient un second moment infini. La conséquence était que la plupart des changements de prix sur une longue période étaient concentrés dans un nombre restreint de jours de trading et c’était là que les fortunes se faisait et se défaisaient. […] Les fractales naturelles montrent des formes de tailles très différentes (allant d’une grande échelle à une échelle inférieure), juste comme les données financières montrent des « cycles » de durées très différentes. »

– Benoit Mandelbrot, Fractals and Scaling in Finance (1997), Benoit Mandelbrot, from Foreword and Preface, page 1.  

Comment mesurer les fractales sur un marché ?

Bien que les fractales demeurent un moyen d’analyse absolument révolutionnaire, les explications à ce sujet demeurent ambiguës et bien généralement complexes. Malgré tout, on peut mesurer le degré fractal d’un actif assez simplement, en deux lignes de calcul. Laissons-nous donc à la pratique d’un exercice relativement simple :

• On suppose que la volatilité mensuelle d’un actif est de 5 %. Si cet actif progresse en moyenne de 2 % par mois, alors plus de deux tiers des variations de cet actif seront comprises entre -3 % (2-5) et +7 % (5+2). 
• On cherche à déduire la volatilité annuelle à partir de cette volatilité mensuelle de 5 %. Dans les modèles probabilistes traditionnels, on multiplie la volatilité mensuelle par la racine de 12 mois dans une année. D’après l’hypothèse de stationnarité, la volatilité annuelle serait de 17 %.
• Cependant, on observe que la volatilité annuelle n’est pas de 17 % mais de 25 %. L’hypothèse de non-stationnarité de Benoît Mandelbrot intervient alors. 

Dans le détail, on annualise d’abord la volatilité d’après l’hypothèse de stationnarité. En d’autres termes, on multiplie la volatilité mensuelle (5) par la racine du nombre de mois qu’il y a dans un an (12). On obtient alors : 

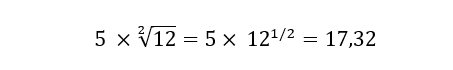
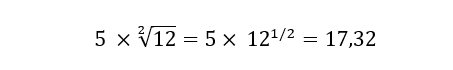
Mais contrairement à ce que suggère le calcul, on observe une volatilité de 25 % par an contrairement à 17 %.On résout alors l’équation suivante en cherchant à définit l’exposant 1/r, qui correspond à l’exposant de Hurst : 

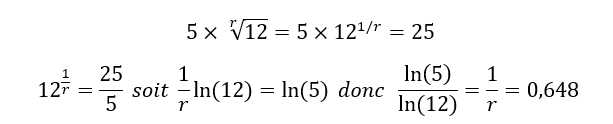
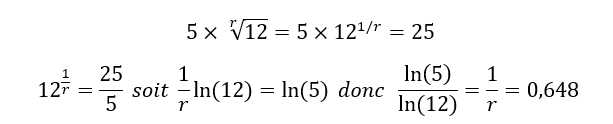
Dans notre cas, l’exposant n’est pas de 0,5 comme dans le modèle, mais de 0,648. Cela implique que l’évolution du cours de l’actif à long terme est déterminée par un nombre restreint de cycles longs (0,648 > 0,5) et qu’il existe véritablement une influence du passé sur les cours futurs. 

Enfin, il est important de rappeler que la formule ln(P)/ln(t) est la généralisation de la formule donnée par Mandelbrot pour estimer la valeur du coefficient de Hurst. 

Quelle stratégie face à l’utilisation des fractales ? 

En effet, la mesure des fractales revient à calculer ce ratio ln(P)/ln(t) qui est une approximation de l’exposant de Hurst. Si l’exposant est supérieur à 0,5 cela revient à écrire que l’actif est régit par des cycles toujours plus déterminants à mesure que le coefficient se rapproche de 1. En termes clairs, cela revient à déduire que :

• Si la valeur du coefficient est inférieure à 0,5 alors l’actif sera soumis à des forces de retournement de marché imminentes ou en cours. En particulier, la plupart des retournements majeurs sur les marchés prennent effet lorsque la valeur du coefficient est proche de 0,3 à moyen terme. 
• Si la valeur du coefficient est supérieure à 0,5 alors l’actif sera soumis à des forces de continuité plus fortes que dans le passé. Cela signifie que l’actif est dans une forte tendance et que la tendance est généralement amenée à se poursuivre. Un excès de tendance (haussier ou baissier) avec un coefficient supérieur à 0,6 est souvent synonyme d’un maximum de performance, ou plus rarement selon les actifs, d’un retournement haussier ou baissier.